Introduction

In this work, we elaborate limitations of fully-connected neural networks and other established approaches like convolutional and recurrent neural networks in the context of reinforcement learning problems that have to deal with variable sized inputs. We employ the structure of Deep Sets in off-policy reinforcement learning for high-level decision making, highlight their capabilities to alleviate these limitations, and show that Deep Sets not only yield the best overall performance but also offer better generalization to unseen situations than the other approaches.

Motivation

A more advanced fixed sized representation considers a relational grid of $\Delta_{\text{ahead}}$ leaders and $\Delta_{\text{behind}}$ followers in $\Delta_{\text{lateral}}$ side lanes around the agent. A relational grid with $\Delta_{\text{lateral}} = 1$ considered side lanes can still be insufficient for optimal decision making, since the white car on the incoming $\Delta_{\text{lateral}}+1$ right lane is not within the maximum of considered lanes, and therefore has no influence on the decision making process.

Technical Approach

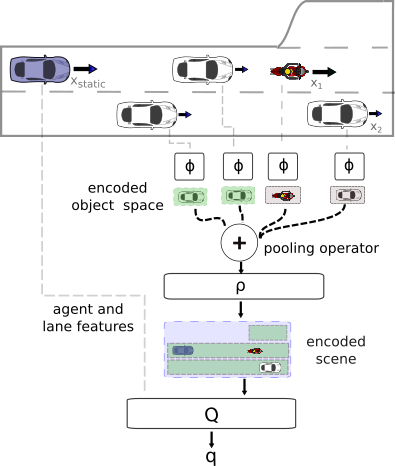
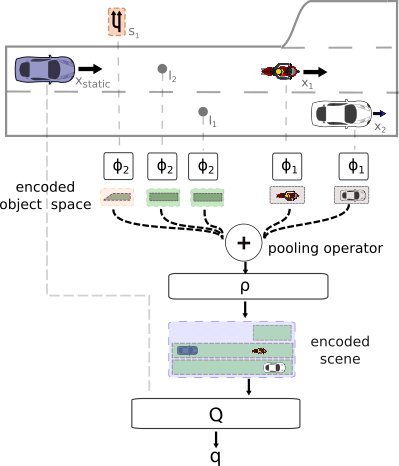
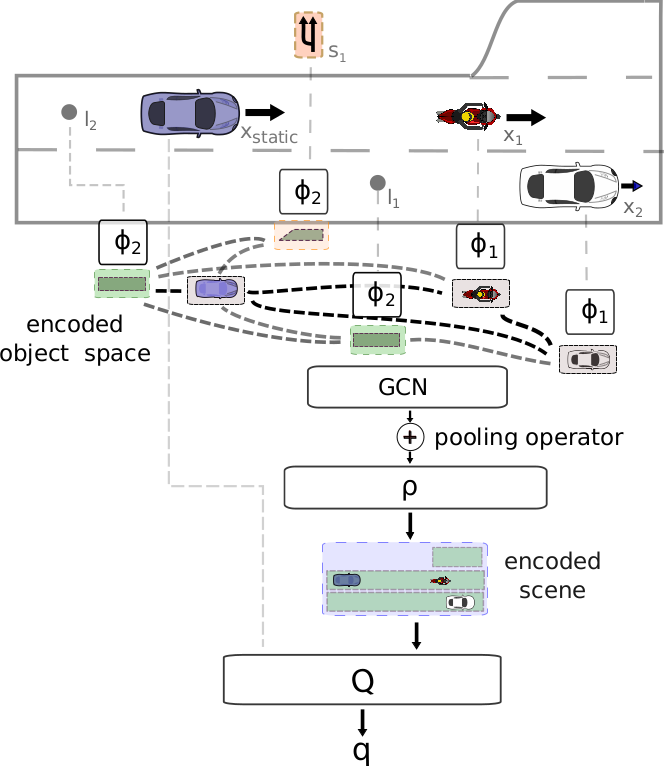
Fig. 2: Scheme of DeepSet-Q algorithm.

We train a neural network $Q_{\mathcal{DS}}(\cdot, \cdot|\theta^{Q_{\mathcal{DS}}})$, parameterized by $\theta^{Q_{\mathcal{DS}}}$, to estimate the action-value function via DQN. The state consists of dynamic input $X_t^{\text{dyn}}=[x^1_t, .., x^{\text{seq len}}_t]^\top$ with a variable number of vectors $x^j_t|_{0\le j \le \text{seq len}}$ and a static input vector $x_{t}^{\text{static}}$. In the application of autonomous driving, the sequence length is equal to the number of vehicles in sensor range. The Q-network $Q_{\mathcal{DS}}$ consists of three main parts, $(\phi,\rho,Q)$. The input layers are built of two neural networks $\phi$ and $\rho$, which are components of the Deep Sets. The representation of the input set is computed by: $$\Psi(X_t^{\text{dyn}}) = \rho\left(\sum_{x^j_t\in X_t^{\text{dyn}}}\phi(x_t^j)\right),$$ which makes the Q-function permutation invariant w.r.t. its input. An overview of the Q-function is shown in Fig. 2, where the static feature representations $x_t^{\text{static}}$ are fed directly to the $Q$-module. The final Q-values are then given by $Q_{\mathcal{DS}}(s_t, a_t)=Q([\Psi(X_t^{\text{dyn}}), x_{t}^{\text{static}}], a_t)$ for action $a_t$. We then minimize the loss function: $$L(\theta^{Q_{\mathcal{DS}}}) = \frac{1}{b}\sum\limits_i\left(y_i - Q_{\mathcal{DS}}(s_i, a_i)\right)^2,$$ with targets $y_i=r_i + \gamma \max_{a} Q'_{\mathcal{DS}}(s_{i+1}, a),$ where $(s_i, a_i, s_{i+1}, r_i)|_{0\leq i \leq b}$ is a randomly sampled minibatch from the replay buffer. The target network is a slowly updated copy of the Q-network. In every time step, the parameters of the target network $\theta^{Q'_{\mathcal{DS}}}$ are moved towards the parameters of the Q-network by step-length $\tau$, i.e. $\theta^{Q'_{\mathcal{DS}}}\leftarrow\tau\theta^{Q_{\mathcal{DS}}} + (1-\tau)\theta^{Q'_{\mathcal{DS}}}$.

Results

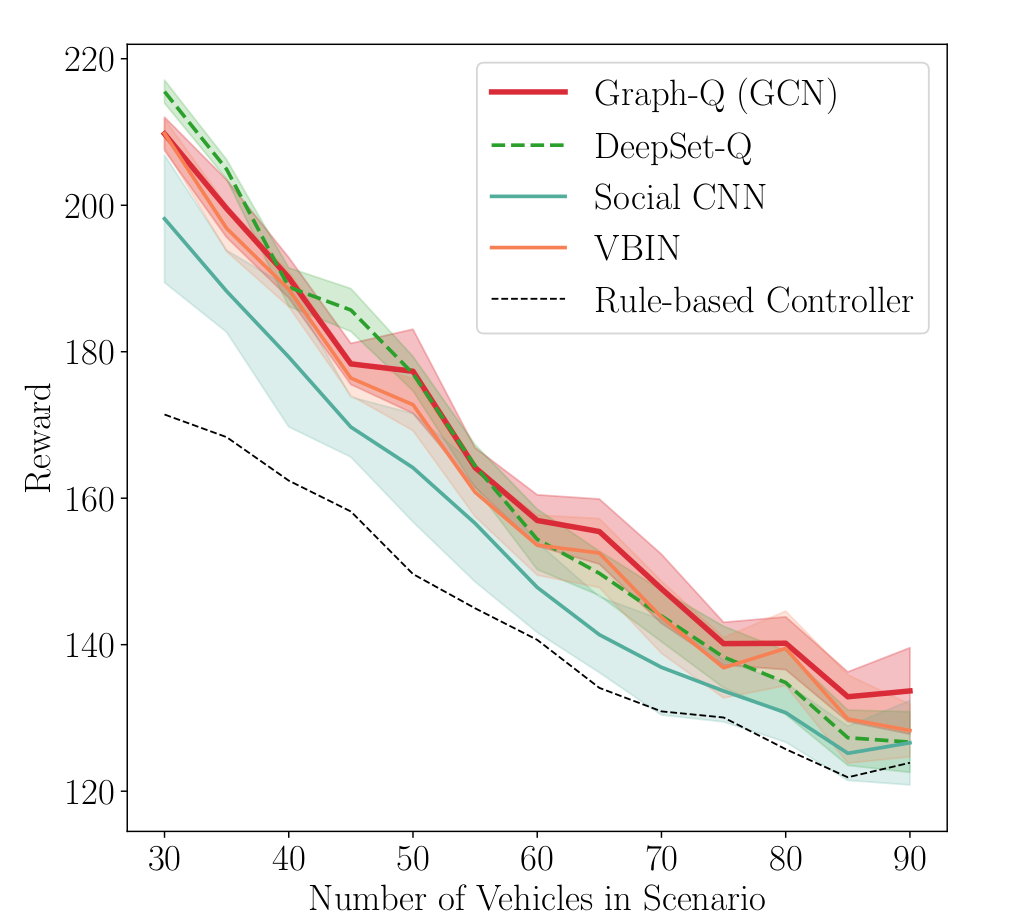
The Deep Set architecture yields the best performance and lowest variance across traffic scenarios in comparison to rule-based agents and reinforcement learning agents using Set2Set, fully-connected or convolutional neural networks as input modules. The results are depicted in Fig. 3. The differences between the approaches get smaller as more vehicles are on the track due to general maneuvering limitations in dense traffic.

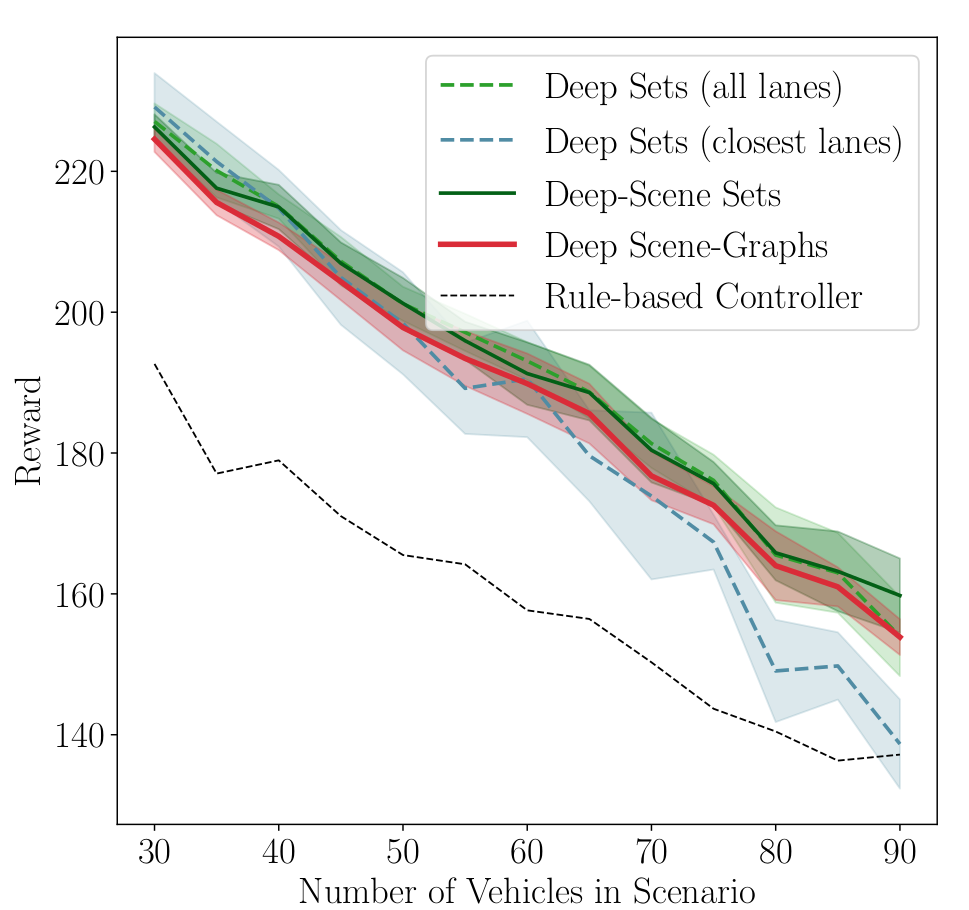
To investigate the generalization capabilities of all methods we trained additionally transitions of at most six surrounding vehicles (see Fig. 4). This is only a small fraction of possible traffic situations. CNNs have difficulties generalizing to unseen situations and suffer from larger variance in comparison to training on the full data set. In contrast, Deep Sets are able to mostly keep the performance even when trained on the truncated dataset, showing only a small increase in variance.

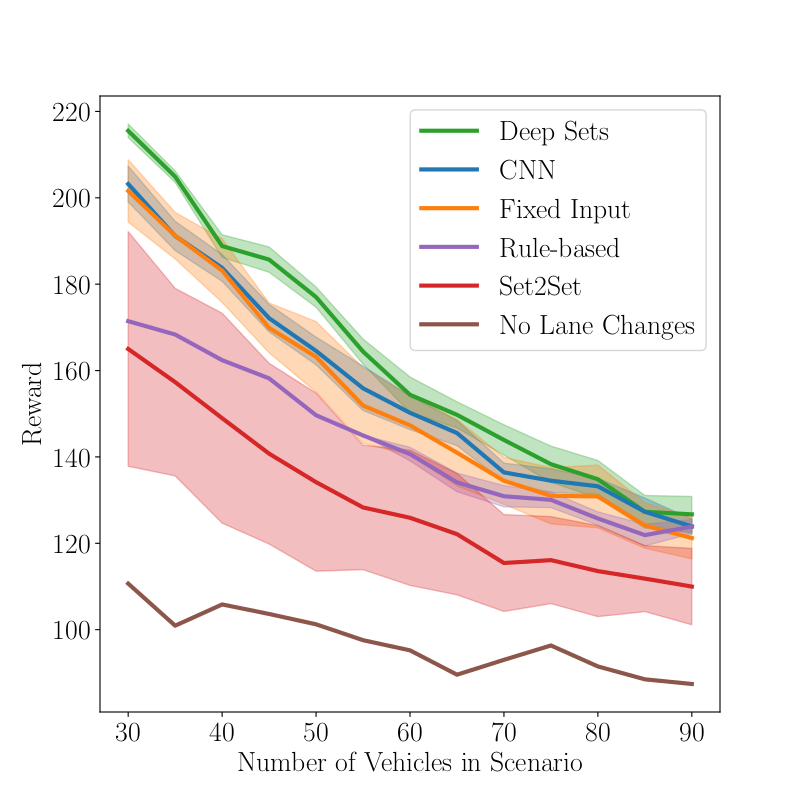
Fig. 3
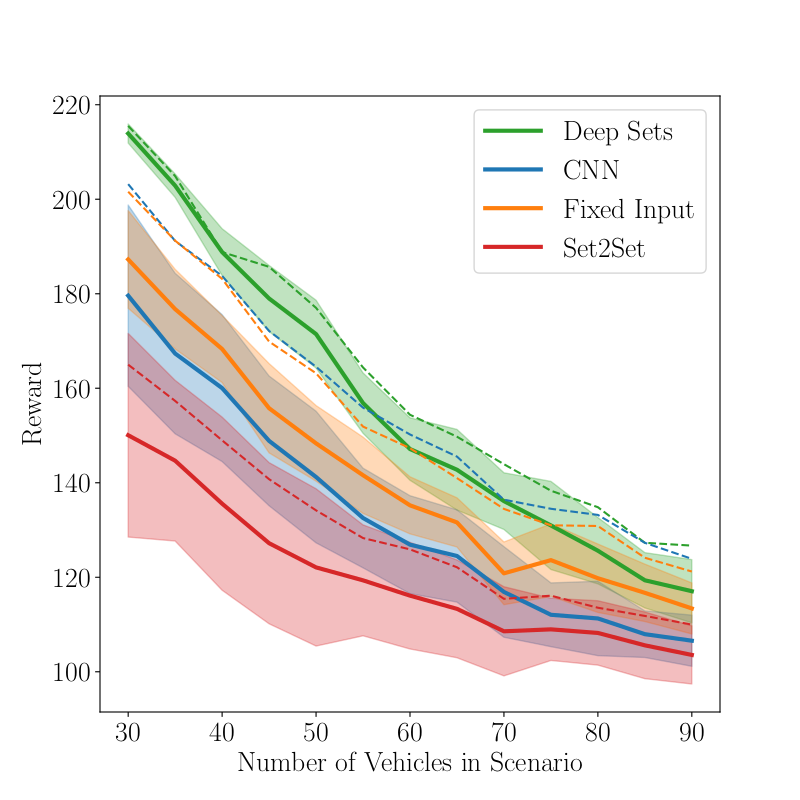
Fig. 4

Results for the DeepSet-Q Algorithm in the Highway scenario when (Fig. 3) trained on the full data set and (Fig. 4) trained on transitions with at most 6 vehicles.

Demonstration

Video explaining methods and performance of DeepSet-Q in the SUMO traffic simulator.

			
@inproceedings{DBLP:conf/iros/HugleKMWB19,
author    = {Maria H{\"{u}}gle and Gabriel Kalweit and Branka Mirchevska
and Moritz Werling and Joschka Boedecker},
title     = {Dynamic Input for Deep Reinforcement Learning in Autonomous Driving},
booktitle = {2019 {IEEE/RSJ} International Conference on Intelligent Robots
 and Systems, {IROS} 2019, 
Macau, SAR, China, November 3-8, 2019},
pages     = {7566--7573},
publisher = {{IEEE}},
year      = {2019},
url       = {https://doi.org/10.1109/IROS40897.2019.8968560},
doi       = {10.1109/IROS40897.2019.8968560},
timestamp = {Fri, 31 Jan 2020 13:28:16 +0100},
biburl    = {https://dblp.org/rec/conf/iros/HugleKMWB19.bib},
bibsource = {dblp computer science bibliography, https://dblp.org}
}
							

Introduction

Our Deep Scenes architecture can learn complex interaction-aware scene representations based on extensions of either 1) Deep Sets or 2) Graph Convolutional Networks. We present the Graph-Q and DeepScene-Q off-policy reinforcement learning algorithms, both outperforming state-of-the-art methods in evaluations with the publicly available traffic simulator SUMO.

Fig. 1: Scheme of DeepScene-Q algorithm using Deep Sets.


Fig. 2: Scheme of DeepScene-Q algorithm using Graph Convolutional Networks.

Motivation

Classical Deep Reinforcement Learning (DRL) architectures like fully-connected or convolutional neural networks (CNNs) are limited in their ability to deal with variable-sized lists of inputs and to model interactions between objects. In previous work, we proposed the DeepSet-Q algorithm, that can deal with a variable list of surrounding cars and was outperforming classical DRL architectures in terms of performance and gereralization to unseen methods. However, this architecture is restricted to a variable-sized list of one object type.

In this work, we propose to use Graph Networks as an interaction-aware input module in reinforcement learning for autonomous driving. We employ the structure of Graphs in off-policy DRL and formalize the Graph-Q algorithm. In addition, to cope with multiple object classes of different feature representations, such as different vehicle types, traffic signs or lanes, we introduce the formalism of Deep Scenes, that can extend Deep Sets and Graph Networks to fuse multiple variable-sized input sets of different feature representations. Both of these can be used in our novel DeepScene-Q algorithm for off-policy DRL.

Technical Approach

Deep Scene-Sets

To overcome the limitation of DeepSet-Q to one variable-sized list of the same object type, we propose a novel architecture, Deep Scene-Sets, that are able to deal with $K$ input sets $X^{\text{dyn}_1}, ..., X^{\text{dyn}_K}$, where every set has variable length. A combined, permutation invariant representation of all sets can be computed by $$ \Psi(X^{\text{dyn}_1}, ..., X^{\text{dyn}_K}) = \rho \left( \sum_{k} \sum_{x \in X^{ \text{dyn}_k}}\phi^k(x) \right),$$ where $1 \le k \le K$. The output vectors $\phi^k(\cdot) \in \mathbb{R}^F $ of the neural network modules $\phi^k$ have the same length $F$. We additionally propose to share the parameters of the last layer for the different $\phi$ networks.

Graphs

We explicitly model relations between vehicles by considering a relational graph of vehicles (nodes) and their interactions (edges). Graph Convolutional Networks (GCNs) use the latent representations $\phi(\cdot)$ as node input features. The edges (relations between the vehicles) are defined manually. An interaction-aware input representation can then be computed by convolutions over the graph.

Deep Scene-Graphs

The graph representation can be extended to deal with multiple variable-length lists of $K$ different object types by using one encoder network for every object type, similar to the Deep Scene-Sets architecture.

Results

In Fig. 3, we compare the performance of the Graph-Q algorithm in the Highway scenario to a rule-based Controller and the DeepSet-Q algorithm. Further, we compare to the interaction-aware Convolutional Social Pooling (SocialCNN) architecture, where A social tensor is created by learning latent vectors of all cars by an encoder network and projecting them to a grid map. Finally, we use Vehicle Behaviour Interaction Networks (VBIN) as a baseline, where instead of summarizing the output vectors as in the Deep Sets approach, the vectors are concatenated.

In Fig. 4, we consider a more complex Fast Lanes scenario with 3 lanes, traffic signs and starting-and ending additional fast lanes. We compare the performance of the Deep Scene-Sets to the Deep Scene-Graphs (that consider a variable number of lanes) with the DeepSet architecture considering a fixed number of surrounding lanes.

Fig. 3: Results for the Graph-Q Algorithm in the Highway scenario.
Fig. 4: Results for the Graph-Q Algorithm in the Highway scenario.

Demonstration

Video explaining methods and performance of DeepScene-Q in the SUMO traffic simulator.

			
@misc{huegle2019dynamic,					
title={Dynamic Interaction-Aware Scene Understanding for 
Reinforcement Learning in Autonomous Driving},		
author={Maria Huegle and Gabriel Kalweit and Moritz Werling and Joschka Boedecker},
year={2019},
eprint={1909.13582},
archivePrefix={arXiv},
primaryClass={cs.LG}
}