Introduction

Fig. 1: SeizureNet demonstration device with a Texas Instruments MSP430FR5994 microcontroller (low power consumption, swift FRAM storage, 256KB memory limit, 8 MHz clock speed). © S.Heller
Implantable, closed-loop devices for automated early detection and stimulation of epileptic seizures are promising treatment options for patients with severe epilepsy that cannot be treated with traditional means. Most approaches for early seizure detection in the literature are, however, not optimized for implementation on ultra-low power microcontrollers required for long-term implantation. In this paper we present a convolutional neural network for the early detection of seizures from intracranial EEG signals, designed specifically for this purpose. In addition, we investigate approximations to comply with hardware limits while preserving accuracy. We compare our approach to three previously proposed convolutional neural networks and a feature-based SVM classifier with respect to detection accuracy, latency and computational needs. Evaluation is based on a comprehensive database with long-term EEG recordings. The proposed method outperforms the other detectors with a median sensitivity of 0.96, false detection rate of 10.1 per hour and median detection delay of 3.7 seconds, while being the only approach suited to be realized on a low power microcontroller due to its parsimonious use of computational and memory resources.

Technical Approach

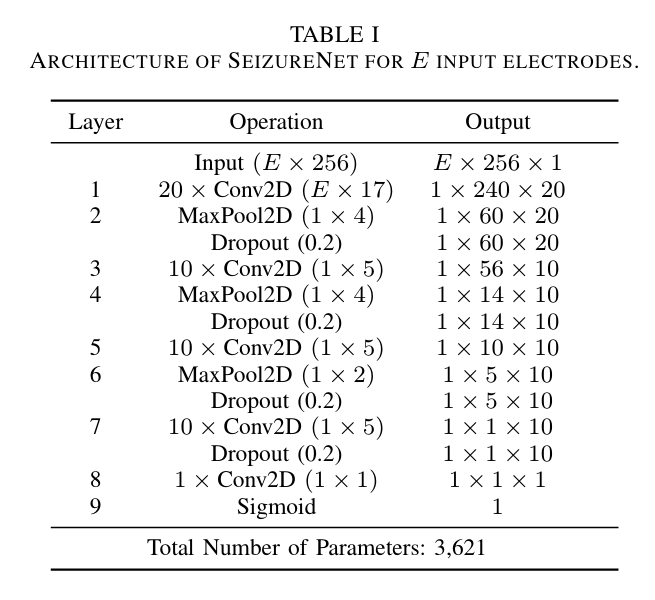
Fig. 2: Architecture of SeizureNet for $E$ input electrodes.

The dataset used is the Epilepsiae database, containing long-term continuous intracranial EEG data. We evaluate our approach on 24 patients. Each recording has a duration between five and eleven days and contains the measurement of approximately 100 intracranial and scalp electrodes originally sampled with or resampled to $f_s = 256\,$Hz. During the two weeks, the evaluated patients had between $6-92$ seizures. To limit the amount of data for our experiments, we consider 100 minutes segments of the recordings around the seizures. For every patient, we consider a subset of $E=4$ electrodes, which are selected a priori by expert epileptologists to cover the seizure onset zone(s). In case that less than four electrodes display the initial ictal EEG pattern, neighboring channels are included for seizure detection. The total number of electrodes is limited due to hardware limitations. In order to find a good model architecture, we evaluated the runtime and memory requirements for various layer types like convolutions, dense layers, pooling layers and activations. The proposed network is a deep convolutional network with alternating convolutional and pooling layers, shown in Fig. 2.

Hardware

For the hardware implementation of the network, a low power microcontroller MSP430FR5994 from Texas Instruments is used, shown in Fig. 1. Due to its power consumption of 118$\,\mu$A/MHz in active mode and 0.5$\,\mu$A in standby mode, it is suitable for the application in an implantable device where a heating of the surrounding tissue must be avoided. A further great advantage of the MSP430FR series is its ferromagnetic nonvolatile memory (FRAM). With a low-power consumption and fast write speed, a swift storage of hidden layer activations of a neural network can be implemented. However, the FRAM also limits the maximum clock speed of the controller as its reading speed is limited to $8$ MHz. It is possible to run the controller with higher clock speeds but only with additional wait states for the CPU leading to a lower power efficiency. Another useful feature for the implementation of convolution layers is the $32$-bit hardware multiplier of the controller, enabling power efficient multiply and accumulate (MAC) operations without CPU intervention.

Seizure Detection Performance Evaluation

It is non-trivial to evaluate a seizure detection system. Mainly, three objectives should be optimized:

• The sensitivity is defined as the ratio of actually detected seizures to the total number of seizures.
• The detection delay is calculated as the mean delay over all detected seizures. For each detected seizure, the delay is defined as the expired time between the electrographic seizure onset identified through visual inspection by a domain expert, and the first algorithm-based detection of the seizure.
• The false positive rate is the number of false detections per hour (fp/h).

Results

The detection performance of SeizureNet is shown in Fig. 3 over all patients, with memory and runtime requirements shown in Fig. 4. With the best median AUC score of $0.89$ and a good balance between false positives and delay, SeizureNet shows the best and most robust detection performance.

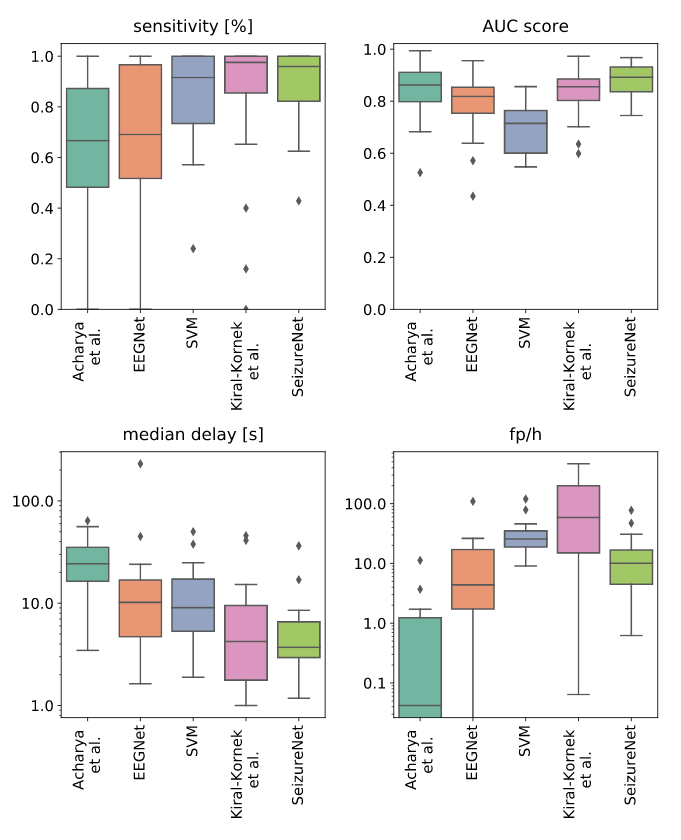
Fig 3: Detection performances over all patients for a classifier threshold of $0.5$.
Median delay and false positive rate are shown in logarithmic scale.
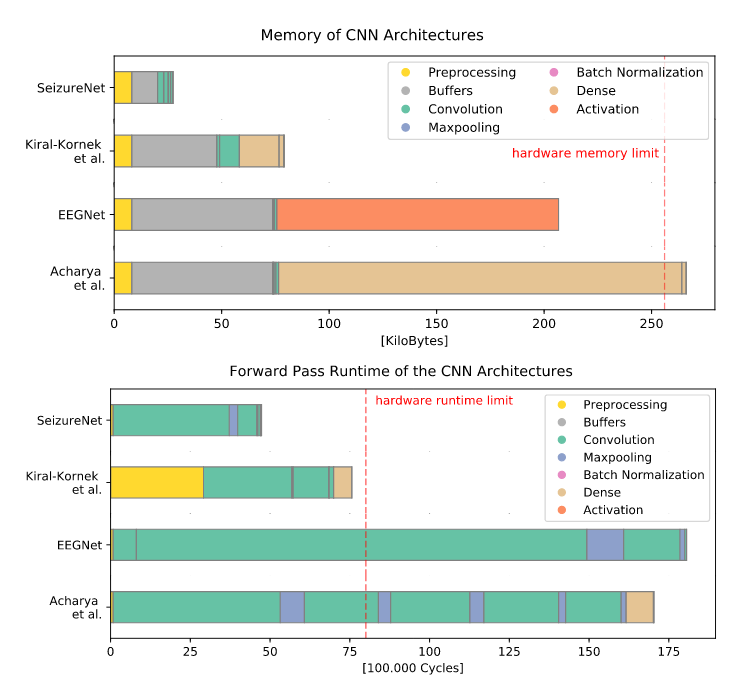
Fig 4: Memory (top) and runtime (bottom) requirements for SeizureNet and the baseline
architectures. Runtime blocks are ordered according to their execution
in the forward pass. Layers with few parameters or cycles are not visible.

The predictions for the repetitive spiking pattern is shown in Fig. 5:

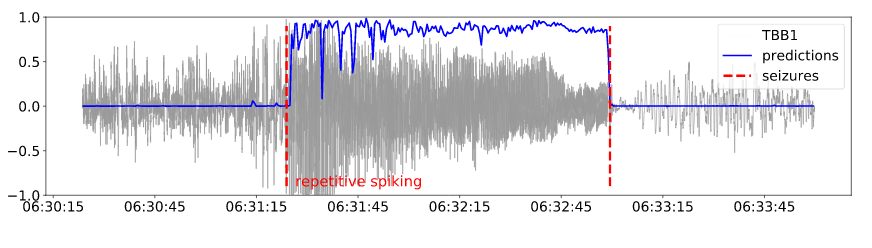
Fig. 5: Early detected seizure with the repetitive spiking onset pattern: predictions one minute
around the seizures and the normalized electrode signal of one electrode.

Demonstration

Video explaining the SeizureNet Demonstration Device.

			
@INPROCEEDINGS{8489493,
author={M. {Huegle} and S. {Heller} and M. {Watter} and 
M. {Blum} and F. {Manzouri} and M. {Duempelmann}
and A. {Schulze-Bonhage} and P. {Woias} and J. {Boedecker}},
booktitle={2018 International Joint Conference on Neural Networks (IJCNN)}, 
title={Early Seizure Detection with an Energy-Efficient Convolutional
Neural Network on an Implantable Microcontroller}, 
year={2018},
volume={},
number={},
pages={1-7},
}
							

Introduction

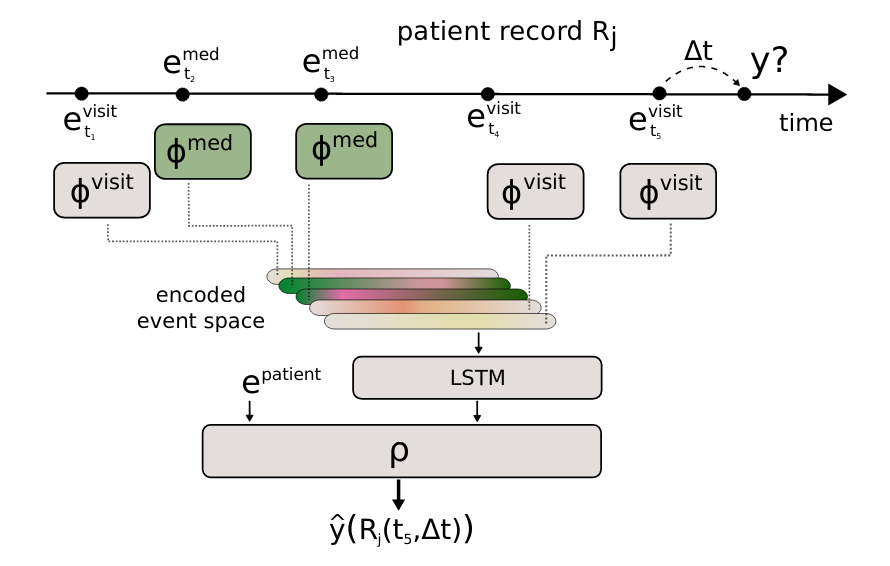Fig. 1: Scheme of AdaptiveNet, which projects visits and medication adjustments to the same latent space using encoder networks $\phi^{\text{visit}}$ and $\phi^{\text{med}}$, where the output vectors $\phi^{(\cdot)}{(\cdot)}$ have the same length. The sorted list of encoded events are pooled by an LSTM to compute a fixed-length encoded patient history. The final output $\hat y$ is computed by the network module $\rho$.}

Clinical data from electronic medical records, registries or trials provide a large source of information to apply machine learning methods in order to foster precision medicine, e.g. by finding new disease phenotypes or performing individual disease prediction. However, to take full advantage of deep learning methods on clinical data, architectures are necessary that 1) are robust with respect to missing and wrong values, and 2) can deal with highly variable-sized lists and long-term dependencies of individual diagnosis, procedures, measurements and medication prescriptions. In this work, we elaborate limitations of fully-connected neural networks and classical machine learning methods in this context and propose AdaptiveNet, a novel recurrent neural network architecture, which can deal with multiple lists of different events, alleviating the aforementioned limitations. We employ the architecture to the problem of disease progression prediction in rheumatoid arthritis using the Swiss Clinical Quality Management registry, which contains over 10.000 patients and more than 65.000 patient visits. Our proposed approach leads to more compact representations and outperforms the classical baselines.

Technical Approach

Disease Progression Prediction

Disease progression prediction based on a clinical dataset can be modeled as time-series prediction, where for a patient at time point $t$ the future disease activity at time point $ t + \Delta t$ is predicted. The dataset consists of records for a set of patients $\mathcal{R} = \bigcup_j \mathcal{R}_j$. Records can contain general patient information (e.g. age, gender, antibody-status) and multiple list of events. The subset $R_j(t) \subseteq \mathcal{R}_j$, denotes all records of a patient $j$ collected until time point $t$ with $$R_j(t) = \{e^\text{patient}(t)\} \cup E^\text{visit}(t) \cup E^{\text{med}}(t),$$ where $e^\text{patient}(t)$ contains general patient information collected until time point $t$. $E^{k}(t)$ is a list of events collected until time point $t$, where $$E^{k}(t) = \{e^{k}(t_e)\ | \ e^{k}(t_e) \in \mathcal{R}_j \text{ and } t_e \le t \} ,$$ for all event types $k \in \{\text{visit}, \text{med}\}$. Visit events contain information like joint swelling or patient reported outcomes (e.g. joint pain, morning stiffness and HAQ) and lab values (e.g. CRP, BSR). Medication events contain adjustment information, such as drug type and dose. In the same manner, further lists of other event types could be added, such as imaging data (e.g. MRI, x-ray).
Considering records $R_j(t)$ as input, we aim to learn a function $ f: (R_j(t), \Delta t) \rightarrow \mathbb{R}$ that maps the records at time point $t$ to the expected change of the disease level $\text{score}_j$ until time $\Delta t$ with $$f( R_j(t), \Delta t) = \text{score}_j(t + \Delta t) - \text{score}_j(t).$$ To account for variable time spans between entries, for all events, the time distance $\Delta t$ to the prediction time point is added as additional input feature. Records with included time feature are denoted as $R_j(t, \Delta t)$ and event lists with $E^{(\cdot)}(t, \Delta t)$. If not denoted explicitly in the following, we assume that $\Delta t$ is included in all records and lists.

AdaptiveNet

Dataset

In this work, we use the Swiss Clinical Quality Management (SCQM) database for rheumatic diseases, which includes data of over 9500 patients with RA, assessed during consultations and via the mySCQM online application. The database consists of general patient information, clinical data, disease characteristics, ultrasound, radiographs, lab values, medication treatments and patient reported outcome (HAQ, RADAI-5, SF12, EuroQol). Patients were followed-up with one to four visits yearly and clinical information was updated every time. The data collection was approved by a national review board and all individuals willing to participate, signing an informed consent form before enrolment in accordance with the Declaration of Helsinki.

Disease Progression Prediction in Rheumatoid Arthritis

To represent the disease level, we use the hybrid score DAS28-BSR as prediction target, which contains DAS28 (Disease Activity Score 28) and the inflammation bloodmarker BSR (blood sedimentation rate). DAS28 defines the disease activity based on 28 joints (number of swollen joints, number of painfull joints and questionnaires (HAQ). For both training and evaluation, we consider only visits with available DAS28-BSR score. We focus on 13 visit features, selected by a medical expert. Additionally, we consider eight medications. As general patient information, we include gender, rheumatoid factor, anti-CCP, time since first symptoms and age.

Results

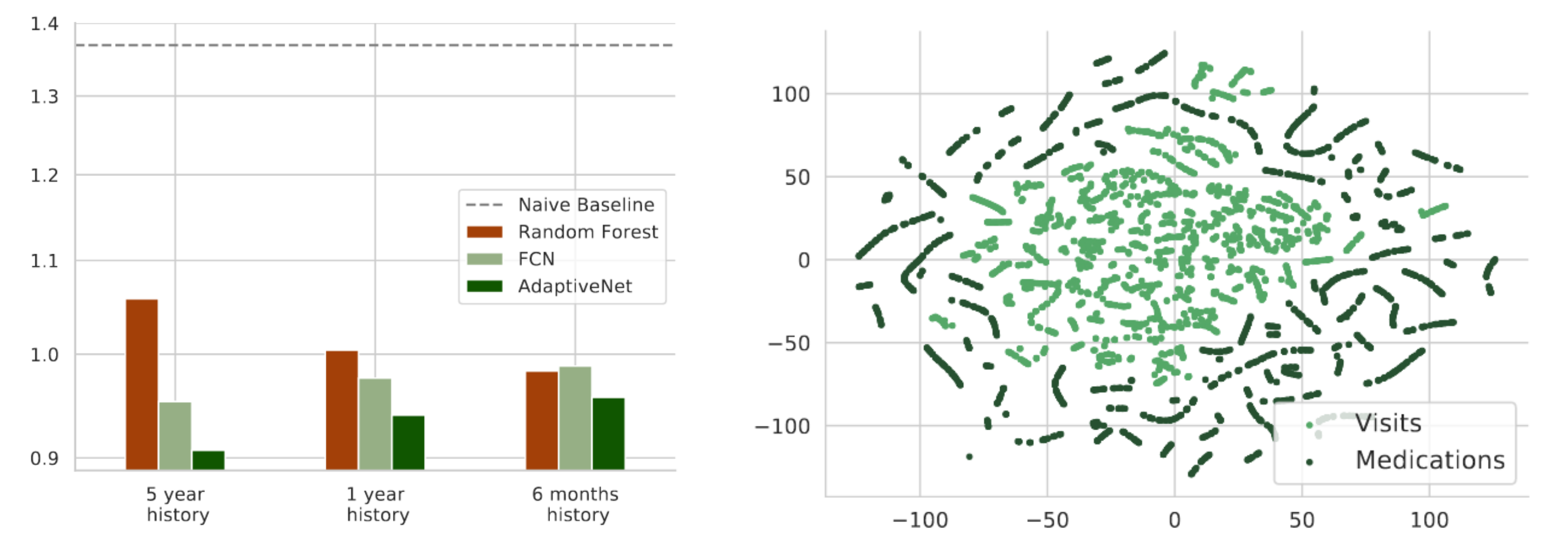Fig. 2: Mean squared error of the disease progression prediction for different maximum history lengths in a range from 5 years
to 6 months. The prediction horizon is 1 year (left). T-SNE visualization of the latent representations $\phi^\text{visit}(\cdot)$ and $\phi^\text{med}(\cdot)$
with shared parameters in the last layer (right).

			
@misc{hgle2020dynamic,
    title={A Dynamic Deep Neural Network For Multimodal Clinical Data Analysis},
    author={Maria Hügle and Gabriel Kalweit and Thomas Huegle and Joschka Boedecker},
    year={2020},
    eprint={2008.06294},
    archivePrefix={arXiv},
    primaryClass={cs.LG}
}